3 - Virtual Pattern Projection
|
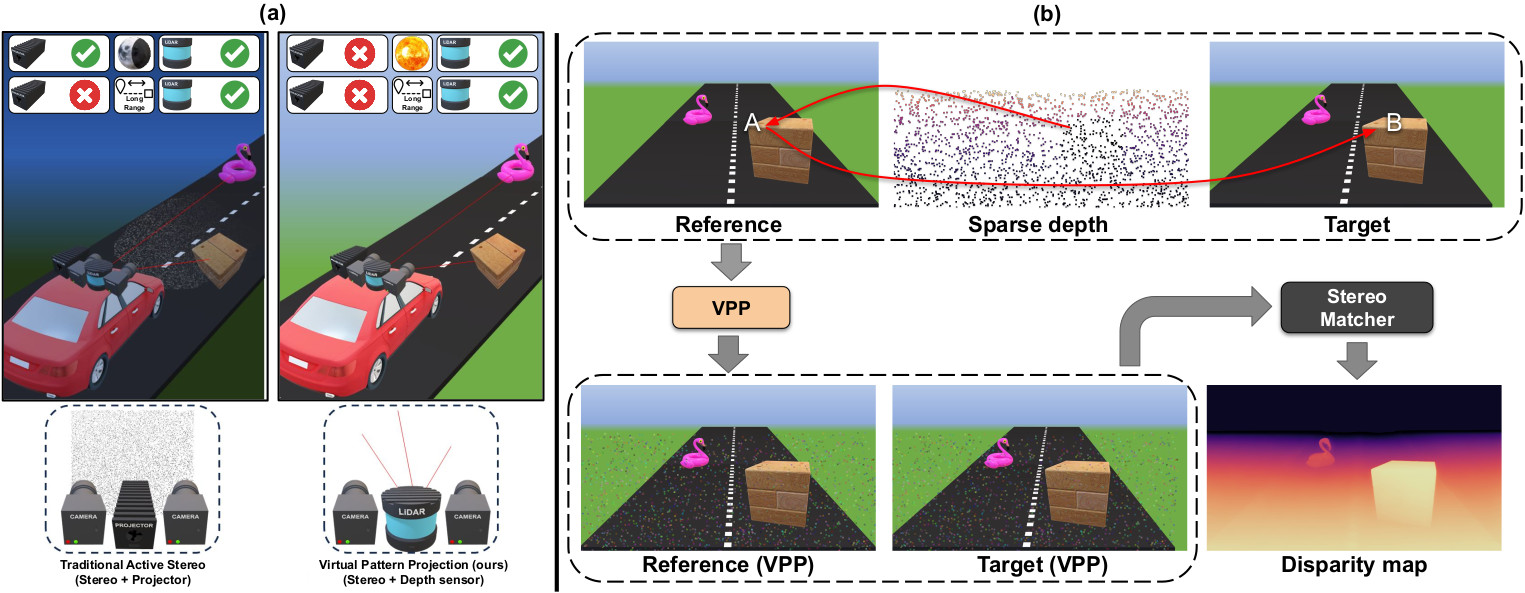
Framework overview.
Given a vanilla stereo pair of images from a stereo camera and sparse depth points from a depth sensor, our framework virtually projects depth seeds to stereo pair according to system geometry and a pattering strategy.
|
As for all fusion methods, our proposal relies on sparse depth seeds but, differentially from them, we inject sparse points directly into images using a virtual pattern.
For each known point, we convert depth into disparity then we apply a virtual pattern in each stereo image accordingly to a pattering strategy.
$$I_L(x,y) \leftarrow \mathcal{A}(x,x',y)$$
$$I_R(x',y) \leftarrow \mathcal{A}(x,x',y)$$
Our method do not require any change or assumption in the stereo matcher: we assume it to be a black-box model that requires in input a pair of rectified stereo images and produce a disparity map.
Augmented stereo pair is less affected by ambiguous regions and makes stereo matcher work easier. Given that our framework alters only stereo pair, any stereo matcher could benefit from it. Since disparity seed could have subpixel accuracy, we use weighted splatting to avoid loss of information.
$$I_R(\lfloor x'\rfloor,y) \leftarrow \beta I_R(\lfloor x'\rfloor,y) + (1-\beta) \mathcal{A}(x,x',y)$$
$$I_R(\lceil x'\rceil,y) \leftarrow (1-\beta) I_R(\lceil x'\rceil,y) + \beta \mathcal{A}(x,x',y)$$
$$\beta = x'-\lfloor x'\rfloor$$
We propose different pattering strategies to enhance distinctiveness and high correspondence, a patch-based approach to increase pattern visibility, alpha-blending with original content to deal with adversial issues with neural networks, a solution to ambiguous projection on occluded points and consequentially an heuristic to classify occluded sparse points. In particular:
-
We propose two different pattering strategies: i) random pattering strategy and ii) distinctiveness pattering strategy based on histogram analysis.
-
Our random strategy is faster than second proposed strategy, but do not guarantee distinctiveness: for each known pair of corresponding points a random pattern is applied in each view, sampling from an uniform distribution.
$$\mathcal{A}(x,x',y)\sim\mathcal{U}(0,255)$$
-
Our histogram strategy performs an analysis in the neighbourood of each corresponding point to guarantee local distinctiveness.
For $(x,y)$ in the reference image, we consider two windows of length $L$ centered on it and on $(x',y)$ in the target image. Then, the histograms computed over the two windows are summed up and the operator $\mathcal{A}(x,x',y)$ picks the color maximizing the distance from any other color in the histogram $\text{hdist}(i)$, with $\text{hdist}(i)$ returning the minimum distance from a filled bin in the sum histogram $\mathcal{H}$
$$\text{hdist}(i) = \big\{\min\{ |i-i_l|,\,|i-i_r| \},i_l\in[0,i[:\mathcal{H}(i_l)>0,i_r\in]i,255]:\mathcal{H}(i_r)>0 \big\}$$
-
Instead of projecting in two single corresponding pixels, a patch-based approach simply assume the same disparity value also for neighbour pixels.
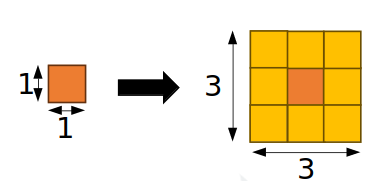
-
The patch can be shaped to fit the context using two strategies: distance based patch-size and RGB guided adaptive patch. The former assumes that things appear smaller in the images at farther distances: a large virtual patch might cover most of a small object when it is far from camera, preventing the stereo algorithm from inferring its possibly different disparity values. Considering a disparity hint $d(x,y)$, a disparity search range $\left[ D_\text{min}, D_\text{max} \right]$, and a maximum patch size $N_\text{max}$, we adjust the patch size $N(x,y)$ as follows:
$$N(x,y) = \text{round}\left( \left(\frac{d(x,y)-D_\text{min}}{D_\text{max}-D_\text{min}}\right)^{\frac{1}{\phi}} \cdot \left( N_\text{max}-1 \right) + 1 \right)$$
where $\phi$ models the mapping curve and $D_\text{min}, D_\text{max}$ are given respectively by the nearest and the farthest hint in the frame.
Regardless of the distance from the camera, a fixed patch shape becomes problematic near depth discontinuities and with thin objects. As detailed next, following Bartolomei et al. we adapt the patch shape according to the reference image content to address this challenge. Given a local window $\mathcal{N}(x,y)$ centered around the disparity hint $d(x,y)$, for each pixel $(u,v)\in\mathcal{N}(x,y)$ we estimate the spatial $S(x,y,u,v)=(x-u)^2+(y-v)^2$ and color $C(x,y,u,v)=\left|I_L(u,v)-I_L(x,y)\right|$ agreement with the reference hint point $(x,y)$ and feed them into model $W_\text{c}(x,y,u,v)$:
$$W_\text{c}(x,y,u,v)=\exp\left(\frac{S(x,y,u,v)}{-2\sigma_s^2}+\frac{C(x,y,u,v)}{-2\sigma_c^2}\right)$$
where $\sigma_s$ and $\sigma_c$ control the impact of the spatial and color contribution as in a bilateral filter. For each pixel $(u,v)$ within a patch centred in $(x,y)$, we apply the virtual projection only if $W(x,y,u,v)$ exceeds a threshold $t_w$. Additionally, we store $W(x,y,u,v)$ values in a proper data structure to handle overlapping pixels between two or more patches -- i.e., we perform virtual projection only for the pixel with the highest score.
-
A virtual pattern might hinder a deep stereo model not used to deal with it. Thus, we combine the original image content with the virtual pattern through alpha-blending.
$$I_L(x,y) \leftarrow (1-\alpha) I_L(x,y) + \alpha \mathcal{A}(x,x',y)$$
$$I_R(x',y) \leftarrow (1-\alpha) I_R(x',y) + \alpha \mathcal{A}(x,x',y)$$
-
Occlusions are an intrinsic product of the stereo system as each view see the scene in a different perspective.
In particular, known depth seeds that are visible in reference view, but occluded in target view could lead to ambiguities.
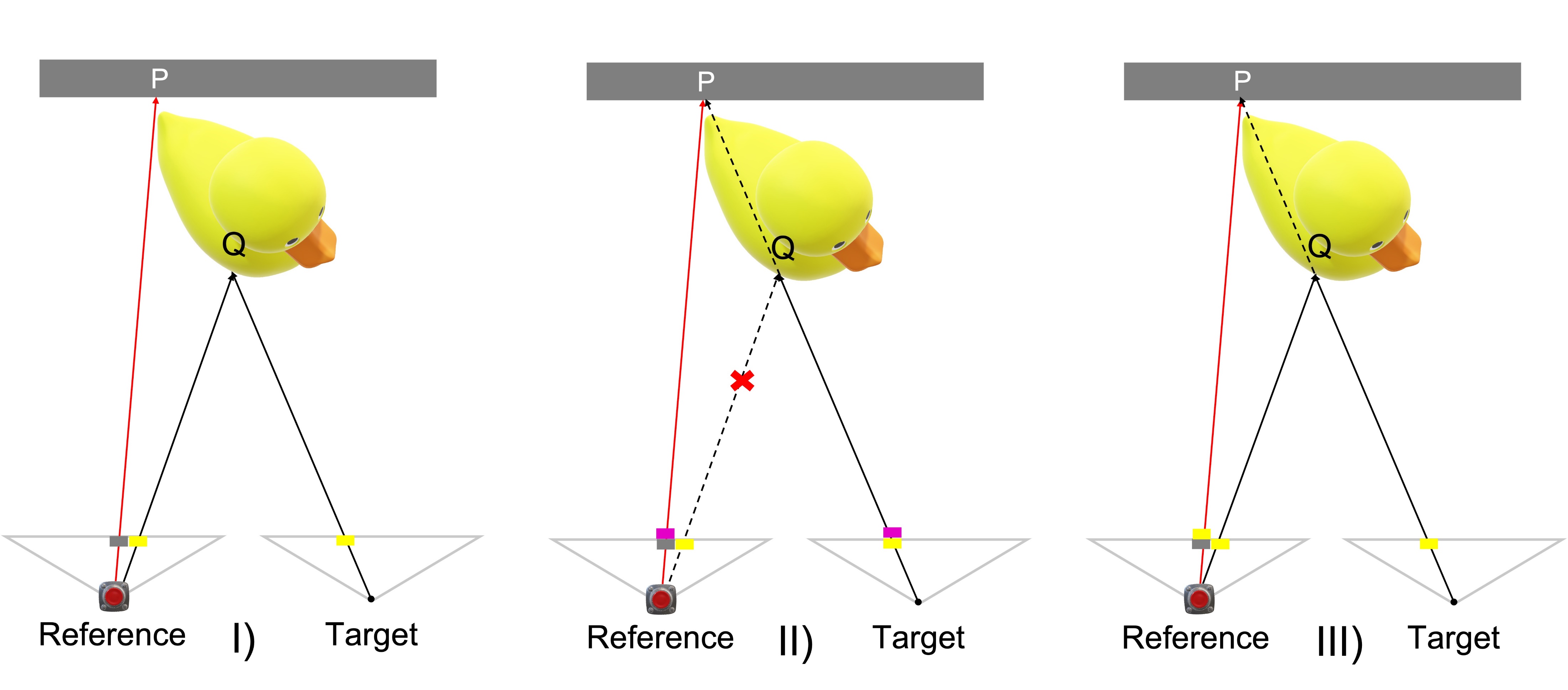
In this example, known point P is virtually projected accordingly to a pattering strategy.
However, as P is occluded in target view, the virtual projection covers original foreground content Q. Consequentially, foreground point has no longer a clear match.
If we can classify correctly P as occluded, we can exploit the potential of our proposal.
Instead of projecting a pattern that would cover foreground content, we can virtually project target content of Q into reference pixel of P.
This solution ease the correspondence for P and do not interfere with foreground pixel.
We propose a simple heuristic to classify occluded sparse disparity points.
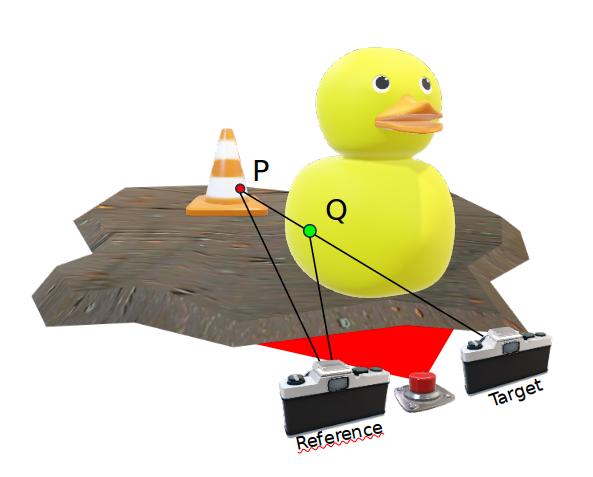
Considering the target view, it assumes at least one foreground sparse point in the neighborhood of the occluded sparse point.
In this example P and Q are known overlapping points in target view, while in reference view they are distinct points.
We aim to classify P as occluded.
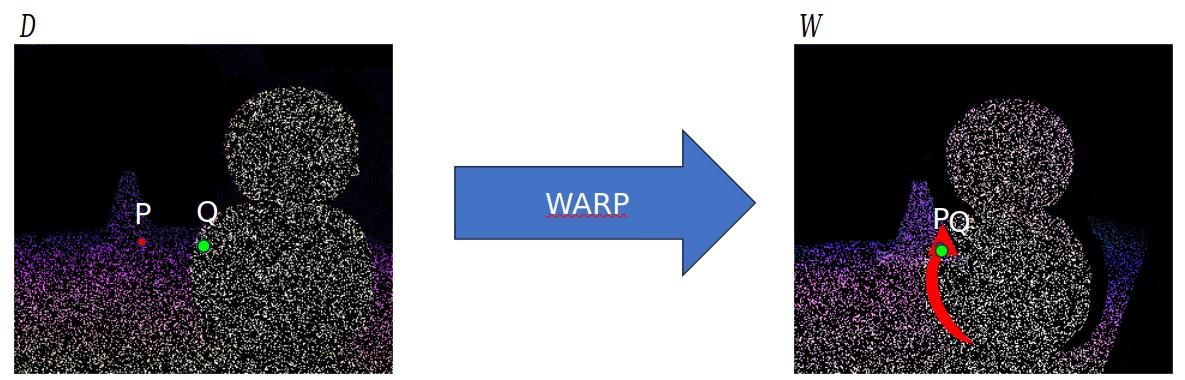
Firstly, given a sparse disparity map obtained using depth sensor, we warp each point at coordinate $(x, y)$ into an image-like grid $W$ at coordinate $(x',y)$.
In this representation sparse points are seen from target view perspective: foreground and occluded points are now closer to each other.
Each valid sparse point $W(x_o,y_o)$ is classified as occluded if the following inequality holds for at least one neighbor $W(x,y)$ within a 2D window of size $r_x \times r_y$.
$$ W(x,y)-W(x_o,y_o) - \lambda (\gamma\lvert x-x_o \rvert + (1-\gamma) \lvert y-y_o \rvert ) > t$$
This inequality simply threshold difference between disparity of two points and weight it accordingly to coordinate distance.
$\lambda$, $t$ and $\gamma$ are parameters that have to be tuned.
Finally, points classified as occluded are warped back to obtain an occlusion mask.

|
VPP in action.
Hallucinated stereo pair using pattern (vi); zoomed-in view with FGD-Projection (a), corresponding area (b) with sub-pixel splatting and left border occlusion projection (c). Adaptive patches guarantee the preservation of depth discontinuities and thin details (d).
|
|